Beam shape corrections to the Law of Reflection

The law of reflection states that with respect to an imaginary line that is perpendicular to the surface of the reflecting object, light will be reflected at the same angle and at the same plane as it was incident.  Euclid, writing in Catoptrics,  already had a  mathematical description of this law in 300 BC [1].

In the 18th century, Isaac Newton conjectured that light can be reflected before hitting the surface [2]. Although not contradicting Euclid, it seems that Newton saw that reflection is not as simple as what Euclid thought.

By the 20th century, researchers began to take a second look at reflection specially since a real physical beam has a finite width. Goos and Hänchen in 1947 reported the first quantitative measurement of a longitudinal shift of the centroid of the beam as in see fig. 1 [3].  A year after, a mathematical description was given by Artmann [4]. This is somewhat similar to the shift that Newton had in mind. However, Goos and Hänchen saw that the reflection with a dielectric happens at the back of the reflection surface. A reflection similar to Newton’s query occurs when the index of refraction is complex such as with metals [5].

A transverse excursion of the beam was also experimentally verified in 1972 (Fig. 2) [6]. This was after a long history of conflicting theories which spans about 60 years. This is called the Imbert-Fedorov effect, named after the experimentalist who first observed it and Fedorov whose initial calculations matched that of Imbert [6,7].

In the last few years, there were also observations of angular deflections in both longitudinal and transverse direction (Fig 3 ) [8,9,10]. This is a real deviation from the law of reflection. These shifts are diffraction corrections to the beam. These deviations are enhanced when the beam is focused.

Now, it is well known that there are four beams shifts that can happen when light is reflected. These are the two longitudinal shifts (positional and angular shifts) and the two transversal shifts (positional and angular shifts). All these shifts are in the order 0.1-10 wavelengths for the positional shifts and micro- to milliradians for the angular shifts.

These shifts might happen together or separately [3-12]. These shifts depend on 1) the polarization of the incident beam; 2) the index gradient seen by the beam; and 3) the degree of the beams’ divergence.

From 2010 to early 2012, our group (my former group) in Leiden University has produced theoretical and experimental publications on the role of the beam’s modal structure to these shifts [13,14,15].

The first of our tasks is to observe how a beam endowed with Orbital Angular Momentum (OAM) affects these shifts [13,14]. A photon of these beams carries  of angular momentum.

The definitive optical beam that carries an OAM is the family of the Laguerre-Gaussian (LG) beam. In the all our experiments, we made use of a home-made HeNe laser that is forced to oscillate higher order Hermite-Gaussian (HG) modes with an intra-cavity wire.  The HG modes are then converted into LG modes with a cylindrical mode converter. The polarization state of the beam is prepared before we let it reflect the prism.  We then measured the deviations from the law of reflection with a quadrant detector [16].

Our results show that the OAM of light couples the four beam shifts (the positional GH and IF shifts and their angular counterparts [13].

The physics behind the angular IF shifts couples with the OAM to produce OAM-dependent GH shifts and conversely, the physics behind the angular GH shifts produces OAM-dependent IF shifts. The angular shifts are enhanced by the OAM of the beam.

We neatly summarized our theoretical results, which are verified by our experiments, with this matrix:

where the  and are the dimensionless positional GH and IF shifts, and the  and are the dimensionless angular GH and IF shifts. The dimensionless parameters are the ones responsible for the shifts upon reflection of a Gaussian beam [13]. Please see note [17].

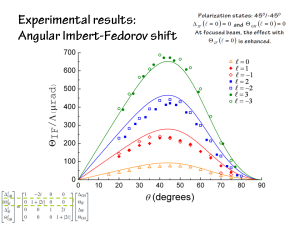
We extended our measurements to higher-order modes () in [14]. Hence, verifying the dependence in .

In our most recent publication, we set out to measure the dependence of these beam shifts to the radial mode index of an LG beam () [15]. The LG beams () form a complete basis set for paraxial light beams. Hence, shifts of different modes can be predicted with the shifts of the LG beams.

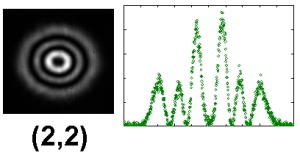
An example of a Laguerre-Gaussian beams with  is shown in figure 7. These beams have extra rings.

The main results of our theory and experiments can be summarized with the matrix:

Notice that the  remains the same but the  has changed. This means that the positional shifts are not changed when but it enhances the angular shifts. Please see note [17].

In summary, we have shown that beam shifts are extrinsically related to the mode of the beam.  Under total internal reflection however, our results are similar to the results of Goos and Hänchen [3] and Imbert [6].For positional shifts, the beam must possess OAM. This is not the case for the angular shifts.

Our results are very important in metrology specifically in the use of higher order modes for gravitational wave detection. On a more fundamental level, it adds to the general understanding of the spin-orbital coupling of different physical systems. The transversal shifts are analogous to the Spin Orbital Hall effect of condensed matter physics.

___________

About the author

Nathaniel Hermosa is currently affiliated with the Institut de Ciencies Fotoniques in Castelldefels (Barcelona), Spain. Prior to this post, he was with the Quantum Optics Group of the Huygens Laboratory, Leiden University, The Netherlands.  He got his PhD in Physics degree from the University of the Philippines Diliman.

During downtime, he writes about science in the Philippines in his blog (http://imphscience.wordpress.com).

___________

Notes:

[1] Hecht, Eugene. Optics. 4th Edition. Addison Wesley, 2002.
[2] Newton, Isaac. Opticks: A Treatise of the Reflexions, Refractions, Inflexions and Colours of Light. London: Royal Society, 1704.
[3] Goos, Hermann Fritz Gustav, and H Hänchen. “Ein neuer und fundamentaler Versuch zur Totalreflexion.” Annalen der Physik 436 (1947): 333-346.
[4] Artmann, K..“Berechnung der Seitenversetzung des totalre?ektierten Strahles.” Ann. Phys. 437 (1948) :87–102.
[5] Merano, M, A Aiello, G W ’t Hooft, M P van Exter, E R Eliel, and J P Woerdman.”Observation of Goos-Hänchen shifts in metallic reflection,” Opt. Express 15 (2007): 15928-15934.
[6] Imbert, Christian. “Calculation and experimental proof of the transverse shift induced by total internal re?ection of a circularly polarized light beam.” Phys. Rev. D 5 (1972): 787–796.
[7] Fedorov, Fedor Ivanovic. “K teorii polnogo otrazheniya.” Dokl. Akad. Nauk SSR 105 (1955): 465.
[8] Hosten, O. and P Kwiat. “Observation of the spin hall effect of light via weak measurements.” Science 319 (2008):787–790.
[9] Merano, M, A Aiello, M P van Exter and J P Woerdman.”Observing angular deviations in the specular reflection of a light beam.” Nature Photonics 3 (2009): 337 – 340.
[10] Aiello, A, and J P Woerdman. “Role of beam propagation in Goos-Hänchen and Imbert-Fedorov shifts.” Optics Letters 33 (2008) : 1437-1439.
[11] Aiello, A, M Merano, and J P Woerdman. “Duality between spatial and angular shift in optical reflection.” Phys. Rev. A 80 (2009):061801.
[12] Merano, M,  N. Hermosa, A. Aiello and J.P. Woerdman. “Demonstration of a quasi-scalar angular Goos–Hänchen effect,” Optics Letters 35 (2010) 3562 – 3564.
[13] Merano, M, N. Hermosa, A. Aiello and J.P. Woerdman. “How orbital angular momentum affects beam shifts in optical reflections”, Phys Rev A 82 (2010) 023817.
[14] Hermosa, N, M. Merano, A. Aiello and J.P. Woerdman, “Orbital Angular Momentum induced beam shifts”, Proceedings of SPIE 7950, 79500F (2011).
[15] Hermosa, N, Andrea Aiello, and J. P. Woerdman, “Radial mode dependence of optical beam shifts,” Optics Letters 37,  (2012) 1044-1046.
[16] Hermosa, N, A. Aiello and J.P. Woerdman, “Quadrant detector calibration for optical vortex”, Optics Letters 36 (2011) 409 – 411.
[17] If a centroid detector is used instead of a median detector, and . For a median detector such as a quadrant detector, , where